Knobelaufgaben, die einen mathematischen Hintergrund haben, werden zahlreich in Büchern und in elektronischen Medien, wie z. B. YouTube, angeboten. Grundsätzlich kann man sich der Lösung auf zwei Wegen nähern: Pfiffige Tüftler*innen werden durch mehr oder weniger gezieltes Probieren zur Lösung kommen. Systematischer und oft auch schneller können Lösungen mathematisch ermittelt werden. Dazu sind im ersten Schritt die linearen Gleichungen mit den gesuchten Unbekannten (Variablen) aufzustellen. Die anschließende Lösung kann per Rechenweg und in grafischer Form gefunden werden. 

In den nachfolgenden Beispielen werden beide Lösungswege je Aufgabe gezeigt.

Aufgabe 1 – Taschengeld

Peter und Thomas bekommen jeden Samstag vom Vater Taschengeld. Peter ist ein Jahr älter und bekommt 2 Euro mehr Taschengeld als sein Bruder Thomas. Zusammen erhalten beide 15 Euro Taschengeld pro Woche.

Wie viel Taschengeld bekommt jeder pro Woche?

Peter = Variable x        

Thomas = Variable y

1. Gleichung

y + 2 = x         | nach y umstellen

y = x - 2

2. Gleichung

x + y = 15        | nach y umstellen

y = 15 - x

Ausdruck für y der 2. Gleichung in 1. Gleichung einsetzen     

x + x - 2 = 15

2x - 2 = 15          | + 2

2x = 17               | : 2

x = 8,5

x in Ausdruck für y einsetzen

y = 15 – 8,5

y = 6,5

Grafische Lösung

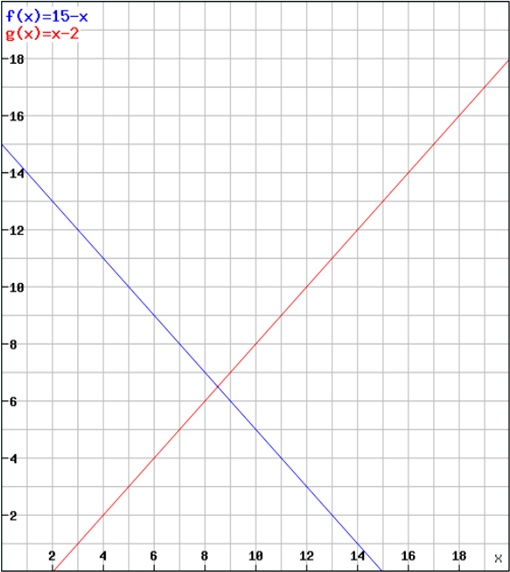
Grafisch dargestellt werden die beiden linearen Gleichungen:

1. Gleichung g(x) = y = x – 2
2. Gleichung f(x) = y = 15 – x

Der Schnittpunkt beider Gleichungen gibt in der Verlängerung auf die jeweilige Achse die Werte für x und y wieder.

Aufgabe 2 – Shoppingtour

Eine Person ist am Wochenende auf Shoppingtour und kauft im Geschäft eine Jeanshose. Im gleichen Geschäft kauft die Person auch noch ein Paar passende Sneaker dazu. Die Schuhe kosten 65,- Euro mehr als die Hose. Der Gesamteinkauf kostet 200,- Euro für die Hose und die Schuhe.

Was kosten die Hose und das Paar Schuhe einzeln?

Hose = Variable x        

Schuhe = Variable y

1. Gleichung

x + y = 200         | nach x umstellen

x = 200 - y

2. Gleichung

y = x + 65

Ausdruck für y der 2. Gleichung in 1. Gleichung einsetzen     

x = 200 - (x + 65)

x = 200 - x - 65              | +x

2x = 200 - 65 = 135       | : 2

x = 67,50          

x in Ausdruck für y einsetzen

y = 67,50 + 65

y = 132,50

Grafische Lösung

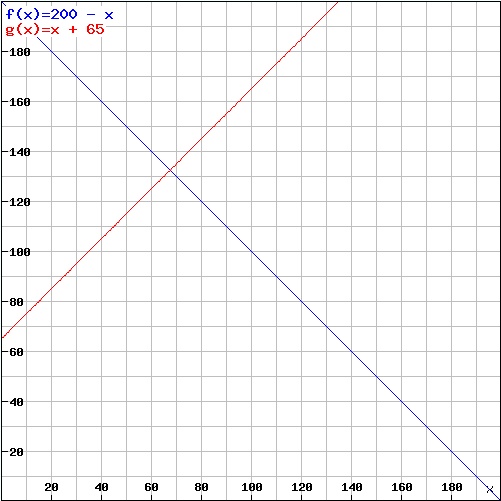
Grafisch dargestellt werden die beiden linearen Gleichungen:

1. Gleichung f(x) = y = 200 - x
2. Gleichung g(x) = y = x + 65

Der Schnittpunkt beider Gleichungen gibt in der Verlängerung auf die jeweilige Achse die Werte für x und y wieder.

Aufgabe 3 – Die Rotweinflasche

Die Herstellung einer Glasflasche für Rotwein kostet 22 Cent mehr als der Korken für die Flasche. Der Korken kostet 8 Cent. Der Rotwein der Flasche hat den hundertfachen Wert des Korkens.

Was muss an der Kasse für die Rotweinflasche gezahlt werden?

Glasflasche = Variable x

Korken = Variable y

Rotwein = Variable z

Gesamtpreis = Variable p

x = y + 22

y = 8

z = 100 * y

p = x + y + z

Wert für y in 1. Gleichung einsetzen     

x = y + 22

x = 8 + 22

x = 30

Wert für y in 2. Gleichung einsetzen     

z = 100 * y

z = 100 * 8

z = 800

Gesamtpreis ist die Addition aller Einzelkosten

Preis = x + y + z

Preis = 30 + 8 + 800 = 838 Cent = 8,38 Euro

Grafische Lösung

y ist eine Konstante. Durch Einsetzen von y ist die 1. und 2. Gleichung ergeben sich x und z, die ebenfalls eine Konstante sind. Die gesuchte Variable p ergibt sich aus den 3 Konstanten x, y und z. Für diesen Sonderfall bedarf es keiner grafischen Lösung.